Logarithmic functions as inverses quiz part 1 embarks on an enlightening journey into the intriguing world of logarithmic functions and their inverse relationship with exponential functions. This quiz delves into the fundamental concepts, properties, and applications of logarithmic functions, providing a comprehensive understanding of their mathematical significance and real-world relevance.

Logarithmic functions, as inverses of exponential functions, possess unique characteristics and exhibit fascinating properties. They play a crucial role in various scientific and engineering disciplines, making them an indispensable tool for solving complex problems and modeling diverse phenomena.

1. Logarithmic Functions as Inverses

Logarithmic functions are the inverses of exponential functions. An exponential function is a function of the form y = a^x, where ais a positive constant. The inverse of an exponential function is a function that “undoes” the exponential function. That is, if y = a^x, then the inverse function is x = log_ay .

For example, the inverse of the exponential function y = 2^xis the logarithmic function x = log₂y . This means that if we plug a value of yinto the exponential function, we get the corresponding value of xby plugging the same value of yinto the logarithmic function.

Properties of Logarithmic Functions, Logarithmic functions as inverses quiz part 1

Logarithmic functions have a number of properties that are related to the properties of exponential functions. Some of these properties include:

• The domain of a logarithmic function is the set of all positive real numbers.
• The range of a logarithmic function is the set of all real numbers.
• The graph of a logarithmic function is a smooth curve that is increasing and concave up.
• The base of a logarithmic function determines the steepness of the graph. The larger the base, the steeper the graph.

2. Graphing Logarithmic Functions: Logarithmic Functions As Inverses Quiz Part 1

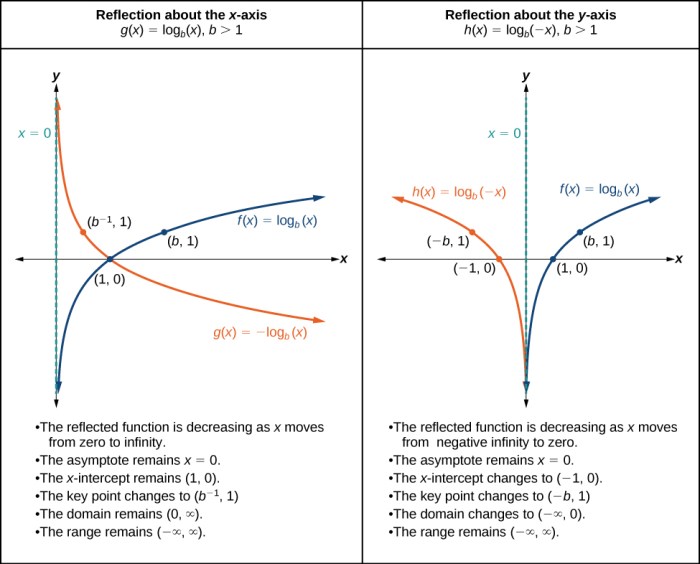
The graph of a logarithmic function can be obtained by reflecting the graph of the corresponding exponential function over the line y = x. This is because the logarithmic function is the inverse of the exponential function.

For example, the graph of the logarithmic function y = log₂x is obtained by reflecting the graph of the exponential function y = 2^xover the line y = x.

The general shape of a logarithmic graph is a smooth curve that is increasing and concave up. The steepness of the graph is determined by the base of the logarithmic function. The larger the base, the steeper the graph.

Transformations of Logarithmic Functions

Logarithmic functions can be transformed in the same way that exponential functions can be transformed. These transformations include:

• Vertical shifts: y = log_a(x) + k
• Horizontal shifts: y = log_a(x – h)
• Reflections over the x-axis: y =-log _a(x)
• Reflections over the y-axis: y = log_a(-x)

FAQ Guide

What is the inverse of a logarithmic function?

The inverse of a logarithmic function is an exponential function.

What are the properties of logarithmic functions?

Logarithmic functions have several properties, including the product rule, quotient rule, power rule, and change of base rule.

What are some applications of logarithmic functions?

Logarithmic functions have numerous applications, including pH calculations, decibel measurements, and growth models.