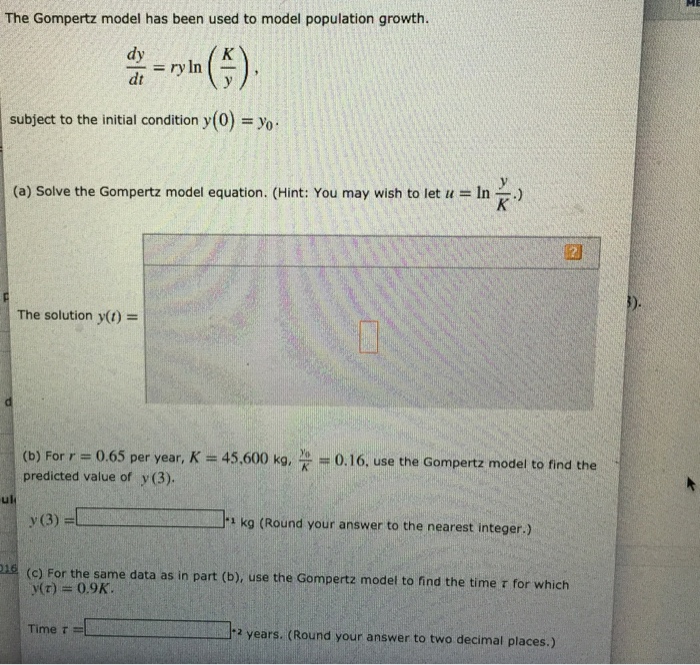
The gompertz model has been used to model population growth. – The Gompertz model has been used to model population growth for decades, providing a valuable tool for understanding and predicting the dynamics of populations. This model captures the characteristic sigmoidal growth curve observed in many biological systems, making it a versatile tool for studying population growth in a wide range of contexts.
The Gompertz model is a differential equation that describes the rate of population growth as a function of the population size and two parameters: the carrying capacity (K) and the growth rate (r). The carrying capacity represents the maximum population size that can be sustained by the environment, while the growth rate determines the rate at which the population approaches the carrying capacity.
1. Gompertz Model Overview
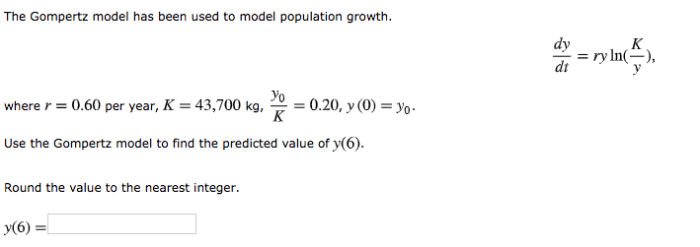
The Gompertz model is a mathematical equation used to describe the growth of a population over time. It is a sigmoid curve that exhibits an initial period of exponential growth, followed by a gradual decline in growth rate as the population approaches its carrying capacity.
The mathematical formulation of the Gompertz model is given by:
$$N(t) = K \cdot e^a \cdot e^-bt$$
where:
- N(t)is the population size at time t
- Kis the carrying capacity, which represents the maximum population size that can be sustained by the environment
- aand bare parameters that determine the shape of the curve
The Gompertz model has been widely used to model population growth in various organisms, including bacteria, insects, and mammals.
2. Factors Influencing Gompertz Model Parameters
Carrying Capacity (K)
The carrying capacity of an environment is determined by a variety of factors, including:
- Availability of resources (e.g., food, water, shelter)
- Competition for resources among individuals
- Predation and disease
- Environmental conditions (e.g., temperature, pH)
Growth Rate (r)
The growth rate of a population is influenced by:
- Birth rate
- Death rate
- Immigration and emigration rates
- Environmental conditions
3. Gompertz Model Applications
Bacterial Growth
The Gompertz model has been successfully used to model the growth of bacterial populations. In this context, the carrying capacity represents the maximum number of bacteria that can be supported by the available nutrients in the environment.
Tumor Growth
The Gompertz model has also been applied to model the growth of tumors. In this application, the carrying capacity represents the maximum size of the tumor that can be sustained by the body’s immune system.
4. Gompertz Model Extensions
Generalized Gompertz Model
The generalized Gompertz model is an extension of the original Gompertz model that allows for more flexibility in the shape of the growth curve. It includes an additional parameter, c, which controls the curvature of the curve.
Gompertz-Makeham Model
The Gompertz-Makeham model is a variant of the Gompertz model that is used to model population growth in the presence of mortality. It includes an additional parameter, d, which represents the mortality rate.
5. Gompertz Model Limitations, The gompertz model has been used to model population growth.
The Gompertz model has some limitations, including:
- It assumes that the growth rate is constant over time.
- It does not account for environmental fluctuations.
- It may not be suitable for modeling populations that experience sudden changes in growth rate.
Despite these limitations, the Gompertz model remains a useful tool for modeling population growth in a variety of contexts.
Question & Answer Hub: The Gompertz Model Has Been Used To Model Population Growth.
What are the assumptions of the Gompertz model?
The Gompertz model assumes that the population growth rate is proportional to the population size and the difference between the population size and the carrying capacity.
What are the limitations of the Gompertz model?
The Gompertz model does not account for environmental fluctuations, density-dependent effects, or other factors that can affect population growth.
How can the Gompertz model be used to predict population growth?
The Gompertz model can be used to predict population growth by solving the differential equation for the population size as a function of time.